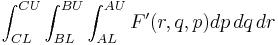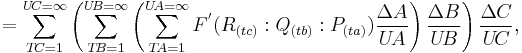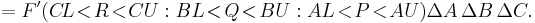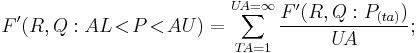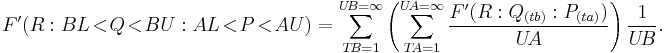Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point ("P") expressible on a graph. The difference between two points, themselves, is known as their Delta (ΔP), as is the difference in their function result, the particular notation being determined by the direction of formation:
- Forward difference: ΔF(P) = F(P + ΔP) - F(P);
- Central difference: δF(P) = F(P + ½ΔP) - F(P - ½ΔP);
- Backward difference: ∇F(P) = F(P) - F(P - ΔP).
The general preference is the forward orientation, as F(P) is the base, to which differences (i.e., "ΔP"s) are added to it. Furthermore,
- If |ΔP| is finite (meaning measurable), then ΔF(P) is known as a finite difference, with specific denotations of DP and DF(P);
- If |ΔP| is infinitesimal (an infinitely small amount—
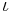 —usually expressed in standard analysis as a limit:
—usually expressed in standard analysis as a limit: 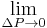 ), then ΔF(P) is known as an infinitesimal difference, with specific denotations of dP and dF(P) (in calculus graphing, the point is almost exclusively identified as "x" and F(x) as "y").
), then ΔF(P) is known as an infinitesimal difference, with specific denotations of dP and dF(P) (in calculus graphing, the point is almost exclusively identified as "x" and F(x) as "y").
The function difference divided by the point difference is known as the difference quotient (attributed to Isaac Newton, it is also known as Newton's quotient):
If ΔP is infinitesimal, then the difference quotient is a derivative, otherwise it is a divided difference:
Contents |
Defining the point range
Regardless if ΔP is infinitesimal or finite, there is (at least—in the case of the derivative—theoretically) a point range, where the boundaries are P ± (.5)ΔP (depending on the orientation—ΔF(P), δF(P) or ∇F(P)):
- LB = Lower Boundary; UB = Upper Boundary;
Derivatives can be regarded as functions themselves, harboring their own derivatives. Thus each function is home to sequential degrees ("higher orders") of derivation, or differentiation. This property can be generalized to all difference quotients.
As this sequencing requires a corresponding boundary splintering, it is practical to break up the point range into smaller, equi-sized sections, with each section being marked by an intermediary point ("Pi"), where LB = P0 and UB = Pń, the nth point, equaling the degree/order:
LB = P0 = P0 + 0Δ1P = Pń - (Ń-0)Δ1P;
P1 = P0 + 1Δ1P = Pń - (Ń-1)Δ1P;
P2 = P0 + 2Δ1P = Pń - (Ń-2)Δ1P;
P3 = P0 + 3Δ1P = Pń - (Ń-3)Δ1P;
↓ ↓ ↓ ↓
Pń-3 = P0 + (Ń-3)Δ1P = Pń - 3Δ1P;
Pń-2 = P0 + (Ń-2)Δ1P = Pń - 2Δ1P;
Pń-1 = P0 + (Ń-1)Δ1P = Pń - 1Δ1P;
UB = Pń-0 = P0 + (Ń-0)Δ1P = Pń - 0Δ1P = Pń;
ΔP = Δ1P = P1 - P0 = P2 - P1 = P3 - P2 = ... = Pń - Pń-1;
ΔB = UB - LB = Pń - P0 = ΔńP = ŃΔ1P.
The primary difference quotient (Ń = 1)
As a derivative
- The difference quotient as a derivative needs no explanation, other than to point out that, since P0 essentially equals P1 = P2... = Pń (as the differences are infinitesimal), the Leibniz notation and derivative expressions do not distinguish P to P0 or Pń:
There are other derivative notations, but these are the most recognized, standard designations.
As a divided difference
- A divided difference, however, does require further elucidation, as it equals the average derivative between and including LB and UB:
- In this interpretation, Pã represents a function extracted, average value of P (midrange, but usually not exactly midpoint), the particular valuation depending on the function averaging it is extracted from. More formally, Pã is found in the mean value theorem of calculus, which says:
-
- For any function that is continuous on [LB,UB] and differentiable on (LB,UB) there exists some Pã in the interval (LB,UB) such that the secant joining the endpoints of the interval [LB,UB] is parallel to the tangent at Pã.
- Essentially, Pã denotes some value of P between LB and UB—hence,
- which links the mean value result with the divided difference:
- As there is, by its very definition, a tangible difference between LB/P0 and UB/Pń, the Leibniz and derivative expressions do require divarication of the function argument.
Higher order difference quotients
Second order
Third order
Ńth Order
Applying the divided difference
The quintessential application of the divided difference is in the presentation of the definite integral, which is nothing more than a finite difference:
Given that the mean value, derivative expression form provides all of the same information as the classical integral notation, the mean value form may be the preferable expression, such as in writing venues that only support/accept standard ASCII text, or in cases that only require the average derivative (such as when finding the average radius in an elliptic integral). This is especially true for definite integrals that technically have (e.g.) 0 and either 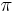 or
or 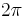 as boundaries, with the same divided difference found as that with boundaries of 0 and
as boundaries, with the same divided difference found as that with boundaries of 0 and 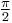 (thus requiring less averaging effort):
(thus requiring less averaging effort):
This also becomes particularly useful when dealing with iterated and multiple integrals (ΔA = AU - AL, ΔB = BU - BL, ΔC = CU - CL):
Hence,
and
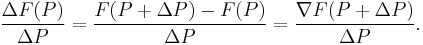
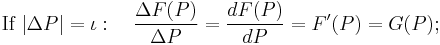
![\mbox{If } |\Delta P| > \mathit{ \iota}: \quad \frac{\Delta F(P)}{\Delta P}=\frac{DF(P)}{DP}=F[P,P%2B\Delta P].\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/0ab05d42e3d1254300700c9afdfd2927.png)
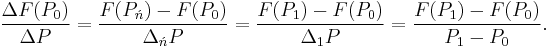
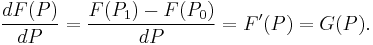
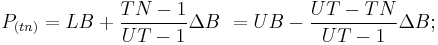
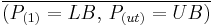
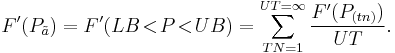
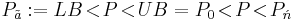
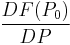
![=F[P_0,P_1]=\frac{F(P_1)-F(P_0)}{P_1-P_0}=F'(P_0\!<\!P\!<\!P_1)=\sum_{TN=1}^{UT=\infty}\frac{F'(P_{(tn)})}{UT},\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/0d3ad8a6347e9019d5e3ed1e2dffaa04.png)
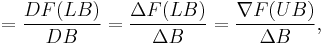
![=F[LB,UB]=\frac{F(UB)-F(LB)}{UB-LB},\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/38139ae668ffb22e0d50d5e673fec533.png)
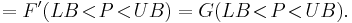
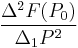
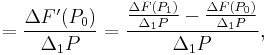
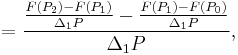
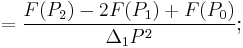
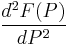
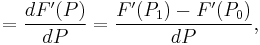
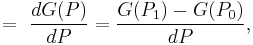
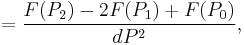
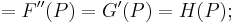
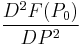
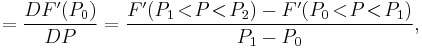
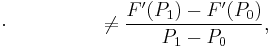
![=F[P_0,P_1,P_2]=\frac{F(P_2)-2F(P_1)%2BF(P_0)}{(P_1-P_0)^2},\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/2234d8237a2cfe15fb16d6455d627011.png)
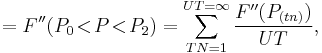
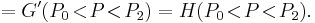
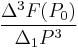
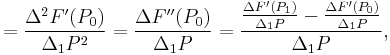
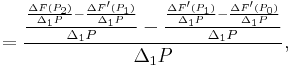
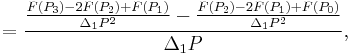
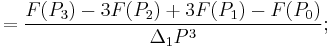
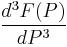
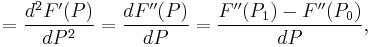
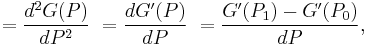
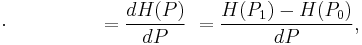
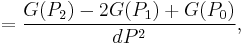
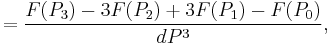
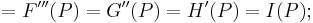
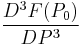
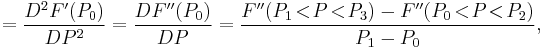

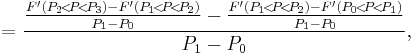
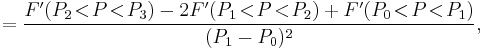
![=F[P_0,P_1,P_2,P_3]=\frac{F(P_3)-3F(P_2)%2B3F(P_1)-F(P_0)}{(P_1-P_0)^3},\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/9aa5ff88e9f843d622984146fd0b629b.png)
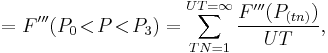
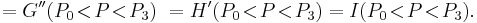
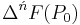
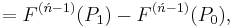
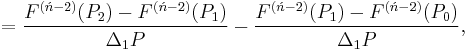
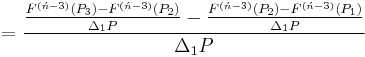
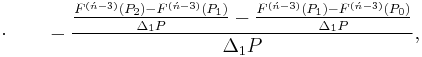

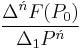
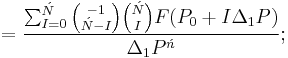
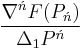
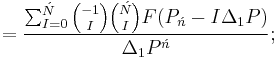
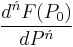
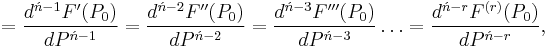
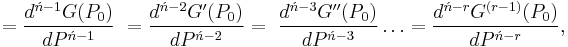
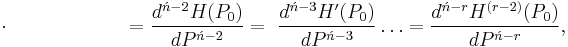
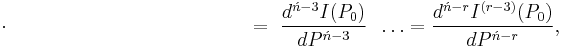
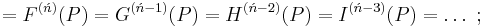
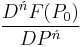
![=F[P_0,P_1,P_2,P_3,\ldots,P_{\acute{n}-3},P_{\acute{n}-2},P_{\acute{n}-1},P_\acute{n}],\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/f82f57c17c230e28788134f8eef5804b.png)
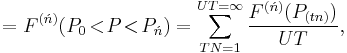
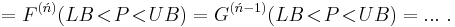
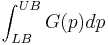
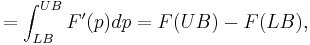
![=F[LB,UB]\Delta B,\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/1a10fe16c034e472cc60f518a347998c.png)
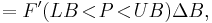
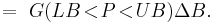
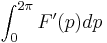
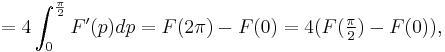
![=2\pi F[0,2\pi]=2\pi F'(0\!<\!P\!<\!2\pi),\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/cdb1618dd00c79eb7944012f34993def.png)
![=2\pi F[0,\begin{matrix}\frac{\pi}{2}\end{matrix}]\;\ =2\pi F'(0\!<\!P\!<\!\begin{matrix}\frac{\pi}{2}\end{matrix}).\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/7cd02c3cda64503f4a9c6627c42dbe96.png)